Tema 2-Circuitos R.L.C en corriente directa
Que es un circuito R.L.C en CD
Un circuito RLC se compone de los elementos pasivos: resistencia, bobina y condensador.
La resistencia representa la oposición
al paso de corriente, la bobina el retardo en el cambio de intensidad y el
condensador la acumulación de carga.
Resistencia: Todos los elementos del circuito que es oponen al
paso de corriente y donde se disipa energía por efecto Joule y su valor depende
de su geometría y de la resistividad ρ (ecuación 1).
R= (l.ρ)/s (1)
Donde l es la longitud, s la sección.
V=I.R (2)
V representa la caída de potencial en la
resistencia debido al paso de corriente.
La ecuación (3) representa la potencia
disipada en la resistencia en función de la caída de potencial en la misma.
Observamos que su valor nunca podrá ser 0, ya que eso equivaldría a una
potencia infinita.
Bobina: Todos los elementos del circuito en los que se acumula y cede energía en forma de campo magnético. El potencial inducido en la bobina, por la Ley de Lenz, viene dado por la expresión:
Con N el número de vueltas de la bobina, Ф el flujo que la atraviesa y L la autoinductancia. Cualquier cambio en el flujo (o sea, en la intensidad) establecerá un voltaje que podrá retardar (que no evitar) el cambio en la intensidad.
La ecuación (5) representa la potencia
absorbida o cedida por la bobina. Como podemos observar, este elemento no
permite un cambio instantáneo (tiempo cero) finito en la intensidad, ya que si
esto ocurriese tendríamos un potencial infinito y eso es imposible.
Condensador: Todos los elementos del circuito donde se almacena y cede energía en forma de campo eléctrico. Se produce una acumulación de cargas en sus placas dando lugar a una diferencia de potencial entre ellas. Se caracteriza (como los resistores por la resistencia R y la bobina por la autoinductancia L) por la capacidad C, la relación entre la carga acumulada y el potencial entre sus placas:
Donde Q es la carga acumulada en las placas y V el potencial entre ellas. La potencia de este elemento viene como:
Donde I se obtiene de la forma diferencial de C=dQ/dV y sabiendo que I=dQ/dt. De forma análoga a los casos anteriores se extrae que en este elemento no puede haber cambios instantáneos de voltaje, ya que eso llevaría como consecuencia un potencial infinito.




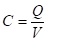



Comentarios
Publicar un comentario