Ejercicios Resueltos, Tema 2-Circuitos R.L.C en corriente directa

 

Problema 1

Calcular los valores de impedancia, intensidad, tensiones en todos los receptores, potencia activa, reactiva y aparente del siguiente circuito en serie RLC:

Empezamos calculando la reactancia inductiva con su fórmula:

Sustituimos los valores de la frecuencia y del coeficiente de autoinducción (en henrios) y operamos:

La reactancia capacitiva la calculamos con la siguiente fórmula:

Sustituimos los datos de la frecuencia y de la capacidad (en faradios) y operamos:

En este circuito, la reactancia inductiva es mayor que la reactancia capacitiva:

Por lo que el triángulo de impedancias queda:

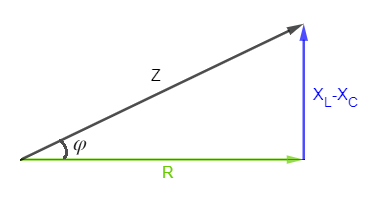
Del triángulo de impedancias obtenemos la fórmula para calcular la impedancia:

Sustituimos los valores de la resistencia, la reactancia inductiva y la reactancia capacitiva y operamos:

Calculamos también el ángulo φ a partir del coseno:

Sustituimos valores de R y Z y operamos:

Realizamos la inversa del coseno y operamos, obteniendo el valor del ángulo φ :

Una vez tenemos calculada la impedancia, podemos calcular la intensidad del circuito dividiendo la tensión total entre la impedancia:

Sustituimos la tensión y la impedancia por sus valores y operamos:

Pasamos ahora a calcular las tensiones del circuito.

La tensión en la resistencia la calculamos multiplicando la intensidad por la resistencia:

Sustituimos valores y operamos:

La tensión en la bobina la calculamos multiplicando la intensidad por la reactancia inductiva:

Sustituimos valores y operamos:

Multiplicamos la intensidad por la reactancia capacitiva para obtener la tensión en el condensador:

Sustituimos valores y operamos:

A partir del triángulo de potencias:

calculamos las diferentes potencias del circuito.

Empezamos calculando la potencia aparente multiplicando la tensión total por la intensidad:

La potencia activa es igual a la potencia aparente por el coseno de φ:

Y la potencia reactiva total la calculamos multiplicando la potencia aparente por el seno de φ:

El diagrama vectorial queda de la siguiente forma:

Problema 2

Un circuito está constituido por un generador de 230 V y 50 Hz y por los siguientes elementos en serie: una resistencia de 25 ohmios, un condensador de 10 microfaradios y una bobina de 0,1 henrios. Calcular la impedancia del circuito y la intensidad del circuito.

Tenemos el siguiente circuito:

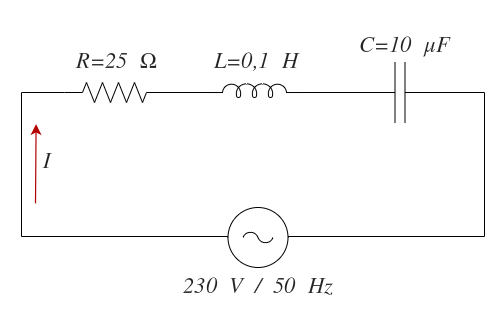
Calculamos la reactancia inductiva:

Y calculamos la reactancia capacitiva:

En este circuito, la reactancia capacitiva es mayor que la reactancia inductiva:

Por lo que el triángulo de impedancias queda:

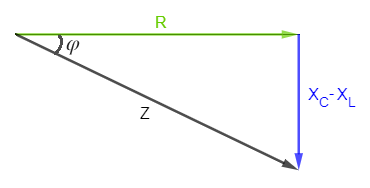
En este caso, la impedancia de se calcula con la siguiente fórmula:

Sustituimos valores y operamos:

Una vez calculada la impedancia, la intensidad de corriente la calculamos con la siguiente fórmula:

Sustituimos valores y operamos:

Problema 3

Un circuito tiene una impedancia de 50 ohmios y un factor de potencia de 0,6 cuando se alimenta con una corriente alterna de 60 hercios, estando el voltaje retrasado respecto a la intensidad.

a) ¿Qué elementos componen el circuito?

b) ¿Qué resistencia ofrece cada uno de ellos?

c) ¿Qué elemento debiera colocarse en serie con él si se desea que su factor de potencia sea 1?

d) ¿Qué características tendrá dicho elemento?

Para saber qué elementos componen el circuito debemos prestar atención a la parte del enunciado donde dice que el voltaje retrasado respecto a la intensidad, lo que nos indica que hay un condensador y que el factor de potencia es 0,6, lo cual nos indica que también hay una resistencia.

Por lo tanto, estamos ante un circuito con una resistencia y un condensador en serie (circuito en serie RC), cuyo diagrama vectorial es:

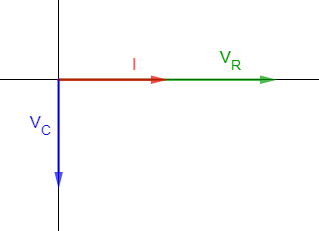
Del dato del factor de potencia, podemos calcular el ángulo φ, ya que el factor de potencia es igual al coseno de φ:

Calculamos φ realizando la inversa del coseno:

Nos ayudamos del triángulo de impedancias de un circuito en serie RC:

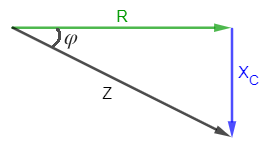
Ya que conocemos el ángulo φ y el valor de la impedancia, podemos calcular la resistencia a partir de la fórmula del coseno:

Despejamos R:

Sustituimos valores y operamos:

El valor de la reactancia capacitiva lo calculamos mediante la siguiente fórmula:

Sustituimos valores y operamos:

Vamos a ver ahora qué elemento necesitamos colocar en serie para que el factor de potencia sea 1.

Que el factor de potencia sea 1, significa que el coseno de φ es igual a 1 y por tanto, si hacemos la inversa del coseno, el ángulo de desfase φ es igual a 0º:

Para conseguir esto, nos fijamos en el triángulo de impedancias de un circuito RLC en serie:

Debemos colocar una reactancia inductiva, que es contraria a la reactancia capacitiva que ya tenemos, para que el lado vertical del triángulo sea igual a 0, es decir, que:

Sustituimos el valor de la reactancia capacitiva en la ecuación anterior:

Y despejamos el valor de al reactancia inductiva:

Por tanto, para que el factor de potencia sea 1, la reactancia total del circuito debe ser 0 y se debe colocar una bobina cuya reactancia inductiva sea del 40 ohmios, es decir, del mismo valor de la reactancia capacitiva que ya tenemos.

Cuando nos preguntan las características de dicho elemento, se refiere a obtener el valor del coeficiente de autoinducción de la bobina.

Para ello, utilizamos la siguiente fórmula:

Sustituimos los valores que ya conocemos:

Y despejamos L: